7. 뉴턴-랩슨법 알고리즘 / 루트값 구하기

21 Jan 2017 . category: Data_Structure . Comments
#korean #theory #data_structure

Newton-Raphson Method

뉴턴-랩슨 법의 이해

뉴턴-랩슨 법(Newton-Raphson Method)을 이용하면 루트값의 근사치 를 구할 수 있다.

최근 들어 루트값을 계산하는 방법에 대해서 궁금해졌는데, 가장 빠르고 정확한 알고리즘으로 뉴턴-랩슨 법을 알게되었다. 가장 빠르고 정확한지는 모르겠지만, 상당히 효율적이고 적은 반복횟수로도 상당한 근사치를 얻을 수 있다는 점에서 좋은 방법이라고 할 수 있다.

뉴턴-랩슨 법의 정의와 증명

먼저 뉴턴-랩슨 법으로 루트값을 구하려면 다음의 점화식을 풀어야한다. \(\sqrt{a}\)를 우리가 구하고자 하는 루트값이라고 할 때,

\[ x_n = {1 \over 2}(x_{n-1} + {a \over x_{n-1}}) \]

\(x_n\)에 아무 숫자나 집어넣고 한 5번만 하면 상당한 근사치가 나온다. 물론 a는 양수만 가능하다. 음수를 집어넣게 된다면 답이없다. 아마 0으로 수렴할 듯 왜 이런 점화식을 풀게 되면 루트값을 구할 수 있는지를 알아보자.

\((\sqrt{k})^2 = k\)이므로 \(\sqrt{k} = x\)라 할 때, \(x^2=k\)라 할 수 있다. 우리는 \(x^2 - k = 0\)의 해를 구해야한다. 해를 구하면, 루트값의 근사값을 알 수 있다. 먼저, \(f(x) = x^2 - k\)의 그래프를 그려보자. 그래프를 대충 그려서 미안하다.

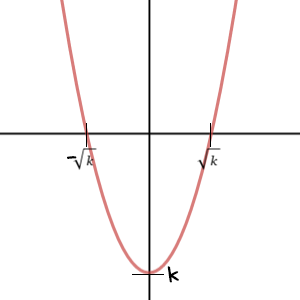
이 그래프를 좀더 확대해보면 다음과 같은 그래프를 볼 수 있다. 설명을 위해 많이 과장된 그래프

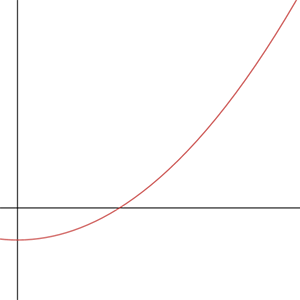
임의의 점 \((a_{n-1}, f(a_{n-1}))\)에서 접선을 그리자. 접선의 함수를 우리는

\[ g(n) = 2a_{n-1}x - ((a_{n-1})^2 + k) \]

라고 할 수 있다. 이 접선의 \(x\)절편을 \((a_{n}, 0)\)이라고 할 수 있고 이 점은 \((a_{n-1}, 0)\) 우리가 처음에 넣었던 임의의 점 보다 \(f(x)\) 그래프의 해에 더 근사함을 볼 수 있다. 다음의 그래프 처럼 말이다.

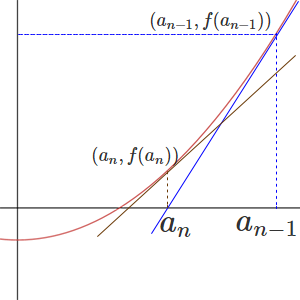
접선의 \(x\)절편을 찾는 과정을 좀더 \((a_{n}, f(a_{n}))\) 일반화하면 점화식은 다음과 같다.

\[ a_n = {1 \over 2}(a_{n-1} + {k \over a_{n-1}}) \]

이 과정을 무한 반복하면 접선의 해(루트값)를 정확하게 구할 수는 없지만 상당히 근사한 값이 나온다.

뉴턴-랩슨 법을 코드로 구현하자!

위의 과정을 알고리즘 (의사코드)으로 간단하게 표현해보자.

1. \(a_1\)의 초기값을 정한다. 구체적으로 정하면 좋지만 대충 해도 알고리즘이 좋아서 괜찮다.
2. 반복횟수를 정한다. 몇가지 예시를 해봤는데, 5번 하면 소수 5자리 까지는 얼추 맞는다.
3. \(a_n = {1 \over 2}(a_{n-1} + {k \over a_{n-1}})\) 점화식에 따라서 반복횟수만큼 반복한다.
4. 결과값을 리턴한다.

이것을 한번 C언어 코드로 구현해보자. 재귀함수로 구현할 것이다. 재귀함수로 구현하면, 비록 속도는 느리지만 코드가 간결하고 가독성이 높아진다. 그렇다는데 난 잘 모르겠다. 속도가 느린건 맞다. 겁나 느리다.

#include <stdio.h>

long double Newton_Raphson(int recoursionNumber, double target) {
	if(recoursionNumber == 0) {
		return 5;
	} else {
		return (Newton_Raphson(recoursionNumber-1, target) + (target/Newton_Raphson(recoursionNumber-1, target)))/2;
	}

}

int main(void) {
	long double root2 = Newton_Raphson(10, 2);
	long double root3 = Newton_Raphson(10, 3);
	long double root5 = Newton_Raphson(10, 5);
	printf("Newton_Raphson 루트%d 값을 구하면 값은 %.15Lf \n", 2, (long double)root2);
	printf("실제 루트2 = 1.414213562373095 // 계산기로 쳐봤다.\n\n");
	printf("Newton_Raphson 루트%d 값을 구하면 값은 %.15Lf \n", 3, (long double)root3);
	printf("실제 루트3 = 1.732050807568877 // 계산기로 쳐봤다.\n\n");
	printf("Newton_Raphson 루트%d 값을 구하면 값은 %.15Lf \n", 5, (long double)root5);
	printf("실제 루트3 = 2.23606797749979 // 계산기로 쳐봤다.\n\n");
}

C언어로 컴파일 해보면 일단 15자리까지는 맞다. 15자리 이상으로 printf문을 만들어봤더니 15자리 이후부터는 0으로 계속 출력되는데 유효소수점이 거기까지 란다. 한, 소수점 80자리까지는 맞춰보고 싶은데 C언어에 어떤 자료형이 있는지 몰라서 그냥 넘어갈란다. 일반적인 상황에서는 15자리 이상 볼 일이 없지 않는가..

이상으로 뉴턴-랩슨 법에 대한 프로그래밍적인 설명을 마치겠다. 뭐, 실제적인 상황에서는 math.h 헤더파일을 사용하면 되겠지만.. 언젠가 루트값을 어떻게 구하지? 하고 의문점이 생길 때, 본 방법을 보면 쉽게 이해할 수 있으리라 생각된다. 개평법 같은건 인간적으로 하지말자…

---